About IMO 2011, problem 6 (bản dịch)

Th1 19

Posted by

Tác giả: Nguyễn Văn Linh

Người dịch: Ong Thế Phương

Hôm nay, chúng ta sẽ trở lại một bài toán thú vị, bài toán như sau:

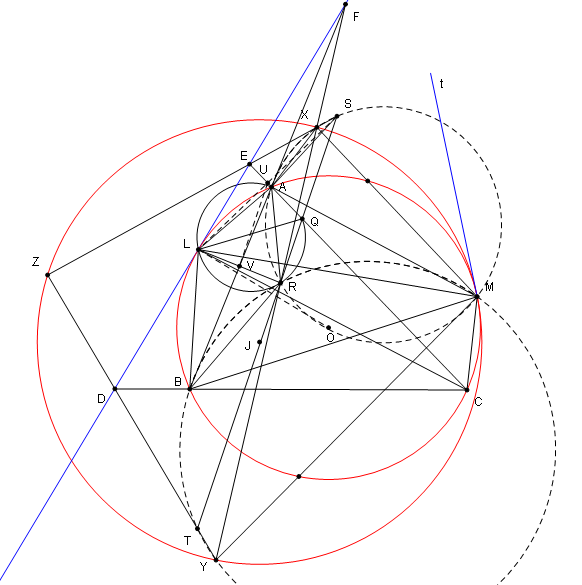
Cho tam giác nhọn ABC nội tiếp đường tròn \Gamma và l là một tiếp tuyến của \Gamma. l_a, l_b, l_c là các đường thẳng đối xứng với l qua BC, CA, AB lần lượt. Chứng minh rằng đường tròn ngoại tiếp của tam giác tạo bởi ba đường thẳng l_a, l_b, l_c tiếp xúc với \Gamma

Chứng minh:

Kí hiệu D, E, F là giao điểm của l với BC, CA, AB lần lượt. Và X, Y, Z là giao điểm của ba đường thẳng l_a, l_b, l_c.

Gọi L là tiếp diểm của \Gamma với l; gọi R, S, T là các điểm đối xứng với L qua AB, AC, BC; M là điểm Miquel của tứ giác toàn phần XSRYTZ

$latex \angle{ZXY} = \angle{FEX} + \angle{EFX} = 180^0 – 2\angle{LEC} + 2\angle{LFA} = 180^0 – 2\angle{BAC}$

Vì khoảng cách từ A xuống l, FY, XZ bằng nhau nên XA là phân giác của \angle{ZXY}

Từ đó nhận được: \angle {ZXA} = \frac{1}{2}\angle {ZXY} = 90^0 - \angle{BAC}. (1)

Mặt khác, gọi U,V là hình chiếu của L lên AC, AB thì $PQ$ đi qua trung điểm của LQ

Ta có: \angle {ARL} = \angle{ARL} = 90^0 - \angle{LUV} = \angle{UQL} điều đó cho ta L, A, Q, R đồng viên. Như vậy: \angle{ARQ} = \angle{LRQ} - \angle{LRA} = 180^0 - \angle{LAQ} - 90^0 + \angle{LAB} = 90^0 - \angle{BAC}.(2)

Từ  (1) và (2) ta nhận được: A \in (XRS). Tương tự với B, C

Vậy thì:

\angle{AMB} = \angle{XMY} - \angle{XMA} - \angle{BMY} = 2\angle{ACB} - \angle{XRA} - \angle{YRB}

= 2\angle{ACB} - 180^0 + \angle{ARB} = 2\angle{CAB} - 180^0 + \angle{ALB} = \angle{ACB}

Như vậy M \in \Gamma.

Dựng tiếp tuyến Mt của (XYZ). Chúng ta sẽ chứng minh Mt cũng là tiếp tuyến của \Gamma bằng cách chỉ ra rằng: \angle{tMA} = \angle{ABM}

\Leftrightarrow \angle{AMX} + \angle{XMt} = \angle{ABR} + \angle{RBM}. (3)

Nhưng: \angle{XMt} = \angle{XYM} = \angle{RBM}, \angle{AMX} = \angle{ARX} = \angle{ALE} = \angle{ABL} = \angle{ABR}

Do đó: (3) đúng (đpcm)

Tổng quát (Trần Quang Hùng):

Cho tam giác ABC và điểm P. Một đường thẳng qua P và cắt các đường tròn (PBC), (PCA), (PAB) lần nữa tại các điểm P_a, P_b, P_c lần lượt. Gọi l_a, l_b, l_c là các tiếp tuyến của (PBC), (PCA), (PAB) tại P_a, P_b, P_c lần lượt. Chứng minh rằng đường tròn ngoại tiếp của tam giác tạo bởi l_a, l_b, l_c tiếp xúc với đường tròn ngoại tiếp tam giác ABC.

Khi P \equiv H, H là trực tâm của tam giác $latec ABC$ chúng ta có bài toán số 6 trong kì thi IMO52.

Chứng minh:

Gọi X, Y, Z là đỉnh các tam giác tạo bởi l_a, l_b, l_c và Q là điểm Miquel của tứ giác toàn phần XYZP_aP_bP_c.

R là giao điểm của AP_c, CP_a.

\angle{ZXY} = \angle{FEX} + \angle{EFX} = 180^0 - 2\angle{LEC} + 2\angle{LFA} = 180^0 - 2\angle{BAC}

Ta sẽ chứng minh L \in (ABC).

Ta có: \angle{P_cAB} + \angle{P_aCB} = \angle{P_cPB} + \angle{P_aPB} = 180^0 nên A, B, C, R đồng viên.

Và \angle{AQC} = \angle{AQP_b} + \angle{CQP_b} = \angle{P_bP_cA} + \angle{P_bP_aC} = 180^0 -\angle{ARC} = \angle{ABC}

Nên Q \in (ABC).

Dựng tiếp tuyến Qt của (XYZ). Ý tưởng của ta là chứng minh Qt cũng là tiếp tuyến của (ABC)  bằng cách chỉ ra: \angle{tQA} = \angle{ACQ}

\Leftrightarrow \angle{tQX} + \angle{XQA} = \angle{ACP_b} + \angle{P_bCQ} (*).

Nhưng: \angle{tQX} = \angle{QZX} = \angle{QCP_b}, \angle{XQA} = \angle{XP_bA} = \angle{QCP_b} nên (*) đúng. Ta có kết luận của bài toán tổng quát.

Posted on 19/01/2012, in Uncategorized. Bookmark the permalink. Bình luận về bài viết này.

Bình luận về bài viết này